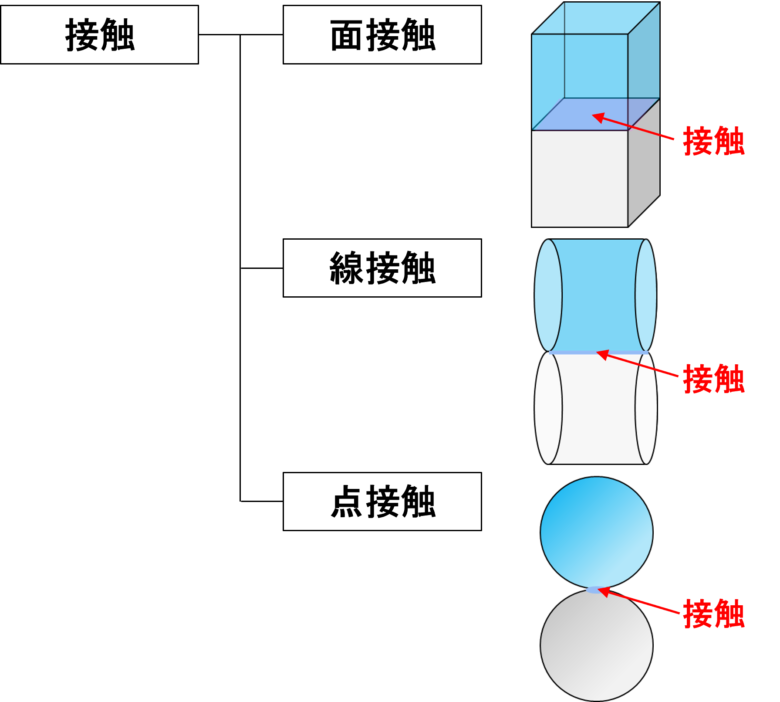
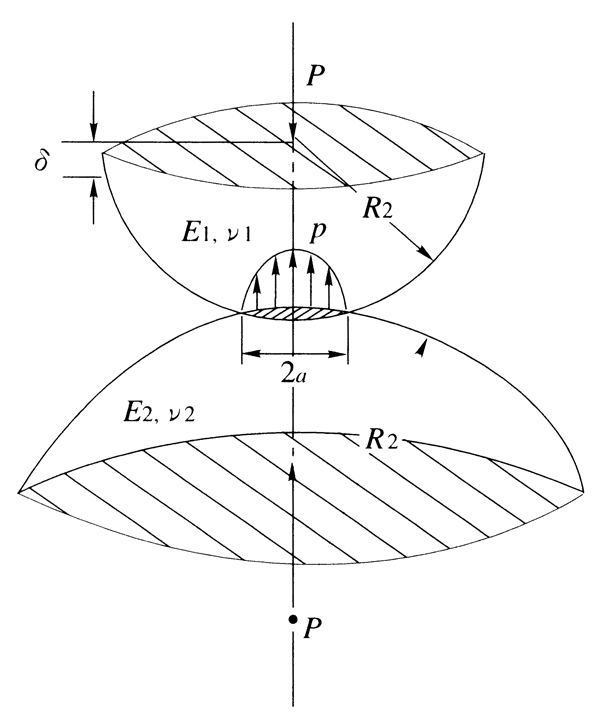
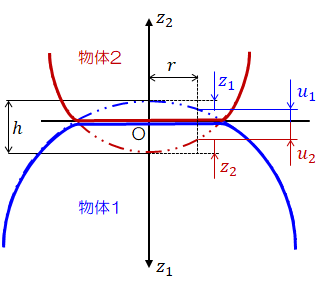
幾何学的に見れば、円と直線の接触は一点です。 力学的には接触部分が相互に弾性的な変形をした狭い幅(面積)で接します。 この幅は、作用する荷重の大きさで変化します。 これを解析的に求
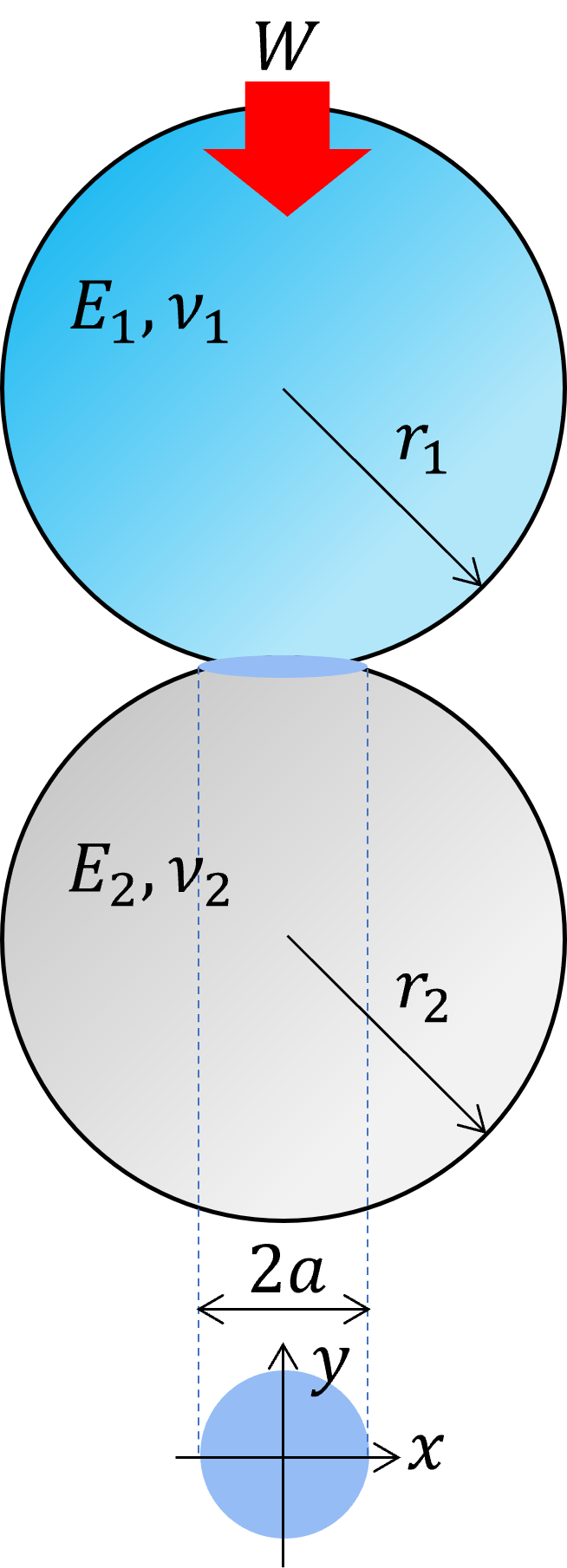
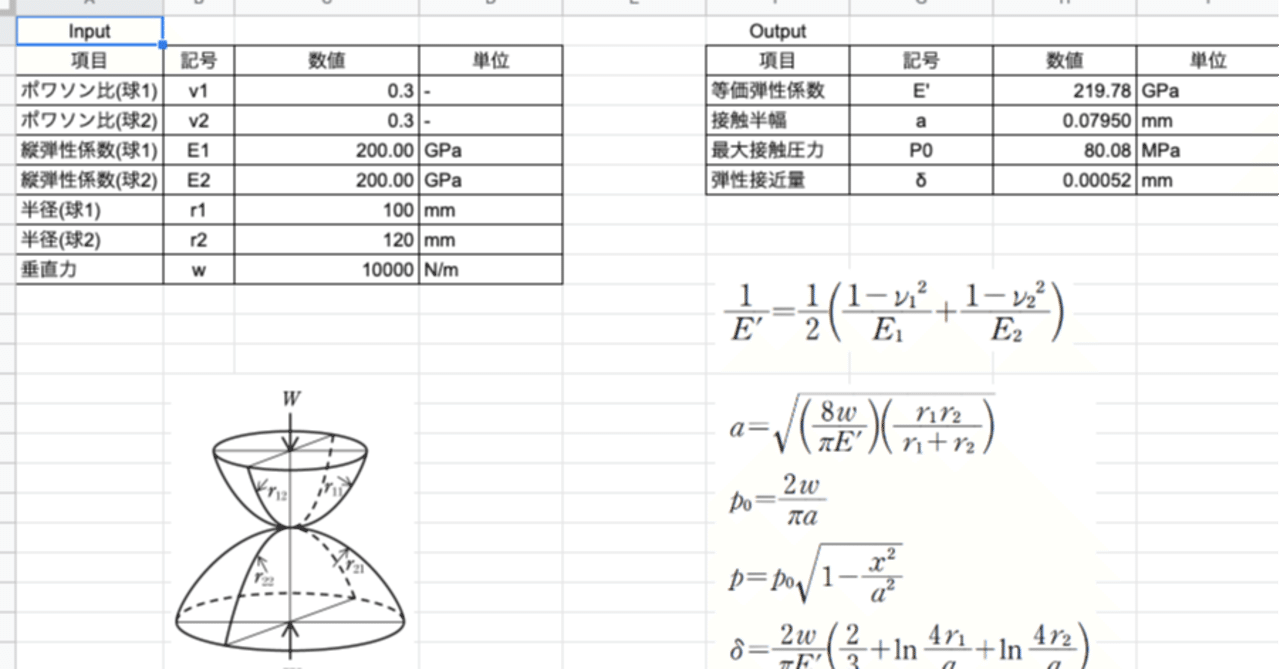
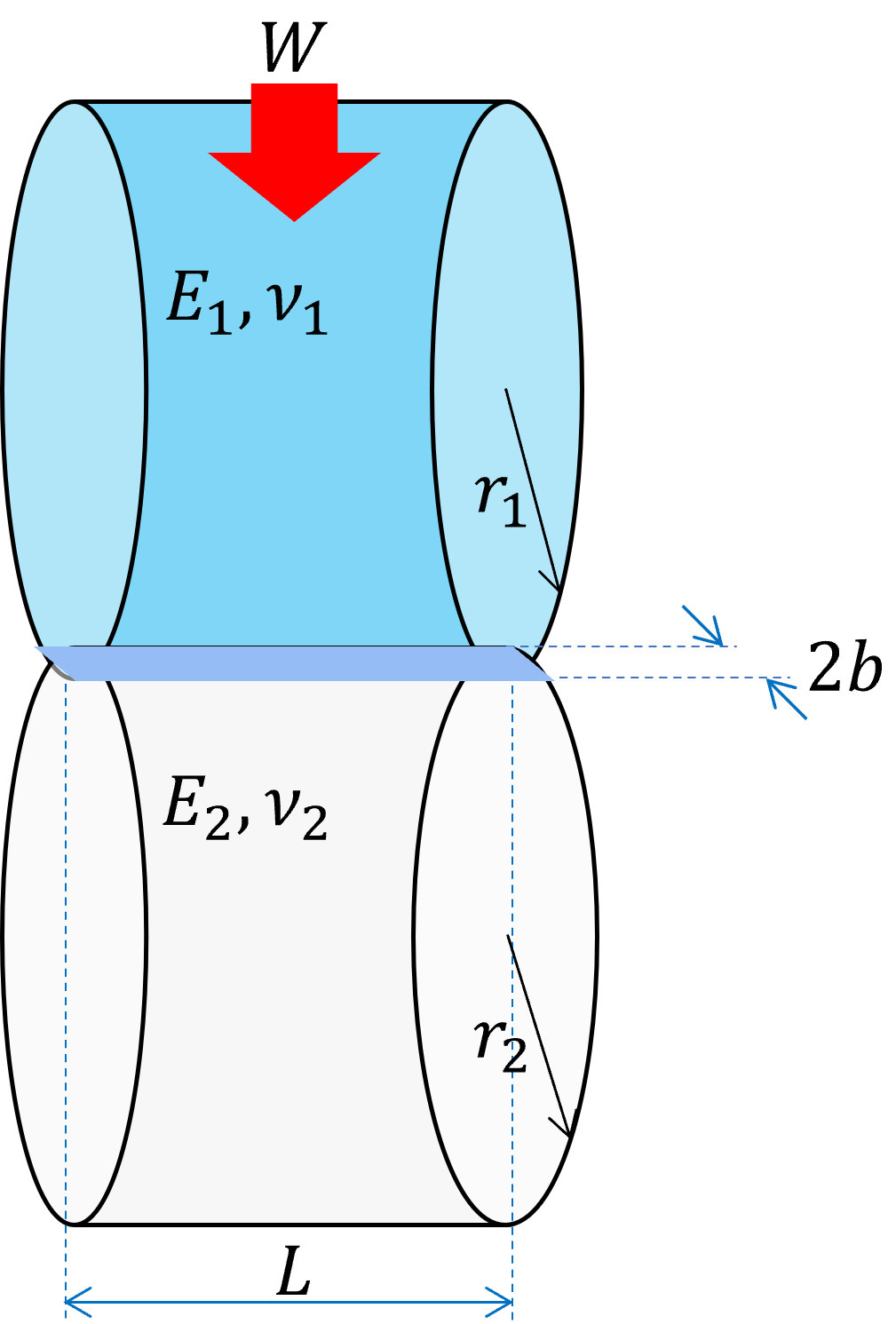
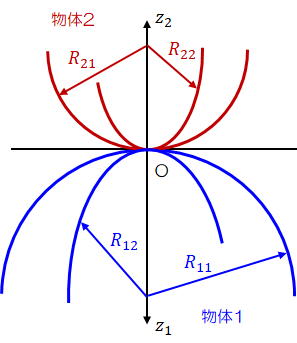
ヘルツ応力 計算式 円柱- いま右図のように球面同士の接触があるとします。 2つの弾性体の曲率半径がr 1, r 2 、ヤング率がE 1, E 2 、ポアソン比がν 1, ν 2 であるとき接触域に対して垂直に荷重Wが印加されボールねじ解析 オンライン計算 ISO 286 によるはめあい公差の計算 はすば歯車の寸法計算 接触応力の計算 深溝玉軸受の計算 マルチレイヤはめあい計算 平歯車の歯底応力計算 ダウンロード
ヘルツ応力 計算式 円柱のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  | |
 | ||
 |  | |
「ヘルツ応力 計算式 円柱」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 |  | |
「ヘルツ応力 計算式 円柱」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「ヘルツ応力 計算式 円柱」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
 |  | |
「ヘルツ応力 計算式 円柱」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
 |  | |
「ヘルツ応力 計算式 円柱」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  | |
 | ||
「ヘルツ応力 計算式 円柱」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
「ヘルツ応力 計算式 円柱」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 | ||
 |  | |
「ヘルツ応力 計算式 円柱」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |
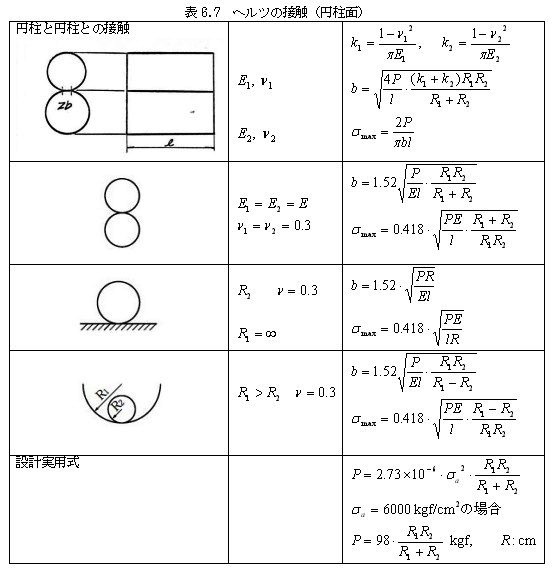
ヘルツの接触応力 (ヘルツのせっしょくおうりょく)は、球面と球面、円柱面と円柱面、任意の曲面と曲面などの 弾性 接触部分に掛かる 応力 あるいは 圧力 のことである。 11年に ハインリヒ・応用した人はヘルツ(Heinrich Rudolf Hertz;独 1857~14)です。ヘルツ理論は、接触問題に多く 貢献しているのですが、論文発表当時は誰も見向 きもされなかったそうです。 では、この論文の
Incoming Term: ヘルツ応力 計算式 円柱,




0 件のコメント:
コメントを投稿